Example demonstrating STAR + DSS

This example shows how one can effectively combine STAR and DSS to recover signal components which would not have been discoverable with either these two techniques alone, due to the presence of strong artifacts.

This example replicates figure 1 in [1].

References

[1]

de Cheveigné A (2016) Sparse Time Artifact Removal, Journal of Neuroscience Methods, 262, 14-20, doi:10.1016/j.jneumeth.2016.01.005

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import leastsq

from meegkit import dss, star
from meegkit.utils import demean, normcol, tscov

# import config  # noqa

rng = np.random.default_rng(9)

Create simulated data

Simulated data consist of N channels, 1 sinusoidal target, N-3 noise sources, with temporally local artifacts on each channel.

# Source
n_chans, n_samples = 10, 1000
f = 2
target = np.sin(np.arange(n_samples) / n_samples * 2 * np.pi * f)
target = target[:, np.newaxis]
noise = rng.standard_normal((n_samples, n_chans - 3))

# Create artifact signal
SNR = np.sqrt(1)
x0 = normcol(np.dot(noise, rng.standard_normal((noise.shape[1], n_chans)))) + \
    SNR * target * rng.standard_normal((1, n_chans))
x0 = demean(x0)
artifact = np.zeros(x0.shape)
for k in np.arange(n_chans):
    artifact[k * 100 + np.arange(20), k] = 1
x = x0 + 10 * artifact


def _sine_fit(x):
    """Fit a sinusoidal trend."""
    guess_mean = np.mean(x)
    guess_std = np.std(x)
    guess_phase = 0
    t = np.linspace(0, 4 * np.pi, x.shape[0])

    # Optimization function, in this case, we want to minimize the difference
    # between the actual data and our "guessed" parameters
    def func(y):
        return np.mean(x - (y[0] * np.sin(t + y[1]) + y[2])[:, None], 1)

    est_std, est_phase, est_mean = leastsq(
        func, [guess_std, guess_phase, guess_mean])[0]
    data_fit = est_std * np.sin(t + est_phase) + est_mean
    return np.tile(data_fit, (x.shape[1], 1)).T

1) Apply STAR

y, w, _ = star.star(x, 2)

proportion artifact free: 0.70
proportion artifact free: 0.70
proportion artifact free: 0.70
depth: 1
fixed channels: 10
fixed samples: 299
ratio: 1.01
power ratio: 0.40

2) Apply DSS on raw data

c0, _ = tscov(x)
c1, _ = tscov(x - _sine_fit(x))
[todss, _, pwr0, pwr1] = dss.dss0(c0, c1)
z1 = normcol(np.dot(x, todss))

3) Apply DSS on STAR-ed data

Here the bias function is the original signal minus the sinusoidal trend.

c0, _ = tscov(y)
c1, _ = tscov(y - _sine_fit(y))
[todss, _, pwr0, pwr1] = dss.dss0(c0, c1)
z2 = normcol(np.dot(y, todss))

Plots

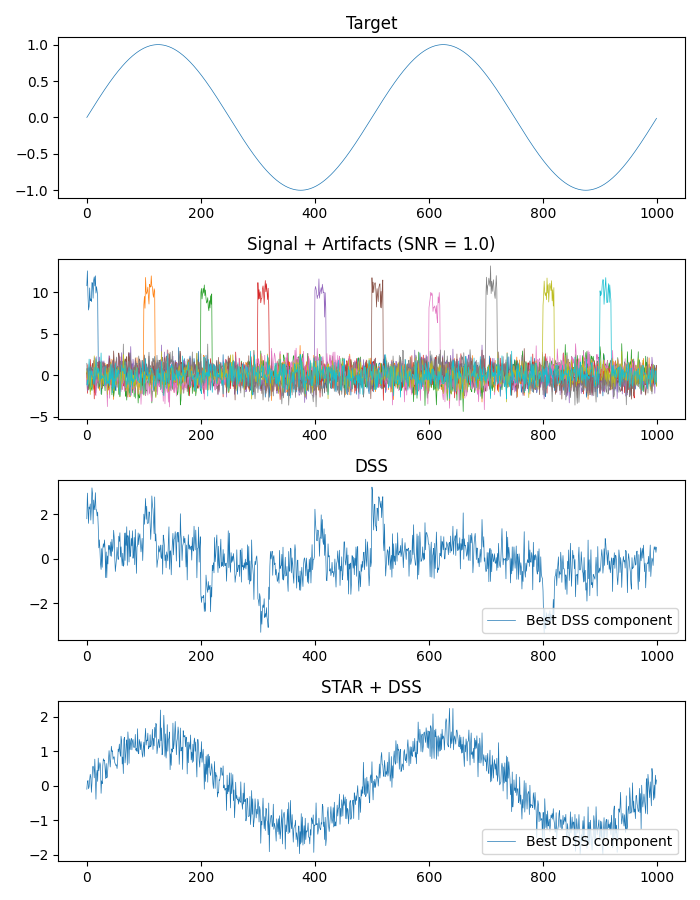
f, (ax0, ax1, ax2, ax3) = plt.subplots(4, 1, figsize=(7, 9))
ax0.plot(target, lw=.5)
ax0.set_title("Target")

ax1.plot(x, lw=.5)
ax1.set_title(f"Signal + Artifacts (SNR = {SNR})")

ax2.plot(z1[:, 0], lw=.5, label="Best DSS component")
ax2.set_title("DSS")
ax2.legend(loc="lower right")

ax3.plot(z2[:, 0], lw=.5, label="Best DSS component")
ax3.set_title("STAR + DSS")
ax3.legend(loc="lower right")

f.set_tight_layout(True)
plt.show()